División de un segmento a razón 1:2

Problema

Con el uso de regla y compás, divide un segmento de longitud dada en dos partes de tal manera que una de sus partes sea la mitad de la otra.

Idea para iniciar con la etapa de exploración

La idea es, dado el segemento AB, construir otro segmento que esté dividido en 3 partes iguales, que uno de sus extremos coincida con A, y que el otro extremo (punto E) esté sobre el segmento, como se muestra en el Modelo 1. De esta manera, tenemos que el segmento AE cumple con la condición de que AC está a razón de 1:2 del segmento CE. Esto significa que, la posición en la que debe ubicarse el punto C para dividir al segmento AB como lo describe el problema, es cuando el punto E coincide con B.

Modelo 1

Si movemos el punto C, observaremos que el segmento AE está dividido en 3 partes iguales y solo existe sobre el segmento AB.
Cuando el punto E coincide con B, entonces el segmento AB está dividido en 3 partes iguales. Así, el segmento AC está a razón de 1:2 del segmento CB.

Pasos para la construcción del modelo 1:

Coloca un punto A en el plano.
Coloca un punto B en el plano.
Traza el segmento AB.
Coloca un punto C en el segmento AB.
Traza una circunferencia centrada en C que pase por A (es decir, de radio AC).
Coloca el punto D en la intersección de la circunferencia y el segmento AB.
Traza una circunferencia con centro en D y que pase por C.
Coloca el punto E en la intersección de esta última circunferencia y el segmento AB.

Exploración

Cuando aproximamos el punto E al punto B, el punto C se aproxima a la posición que buscamos llegar con trazos que puedan ejecutarse con regla y compás. Sin embargo, necesitamos una pista que nos permita identificar qué trazos geométricos nos ayudan a hallar la posición precisa en la que debe estar C cuando E está sobre el punto B. Justo aquí, es donde el modelo dinámico puede darnos una pista sobre el tipo de trazos que necesitamos. Unas preguntas que pueden guiarnos son: ¿Qué lugar geométrico describe alguna de las intersecciones entre las circunferencias cuando movemos el punto C sobre el segmento AB? ¿Se pueden obtener los puntos de intersección entre las circunferencias de forma precisa cuando E coincide con B? ¿Podemos trazar el lugar geométrico de forma robusta? Interactúa con el Modelo 2 y luego revisa el video.

Modelo 2

Explicación de la exploración.

Construcción robusta

Entonces, con los siguientes pasos podemos llevar a cabo la construcción robusta o sintética descrita en el problema (ver Modelo 3).

Obtén el punto medio del segmento AB.
Obtén el punto medio del segmento CB.
Traza la perpendicular al segmento AB que pase por D.
Traza la circunferencia centrada en C que pase por un extremo del segmento AB.
Coloca el punto E en la intersección de la circunferencia y la mediatriz de CB.
Traza el segmento AE.
Traza la mediatriz de AB.
Coloca el punto F en la intersección de la mediatriz de AB y el segmento AE.
Obtén el punto medio del segmento AF.
Traza la perpendicular al segmento AE que pase por G.
Coloca un punto H en la intersección de la mediatriz AF con el segmento AB.

Modelo 3

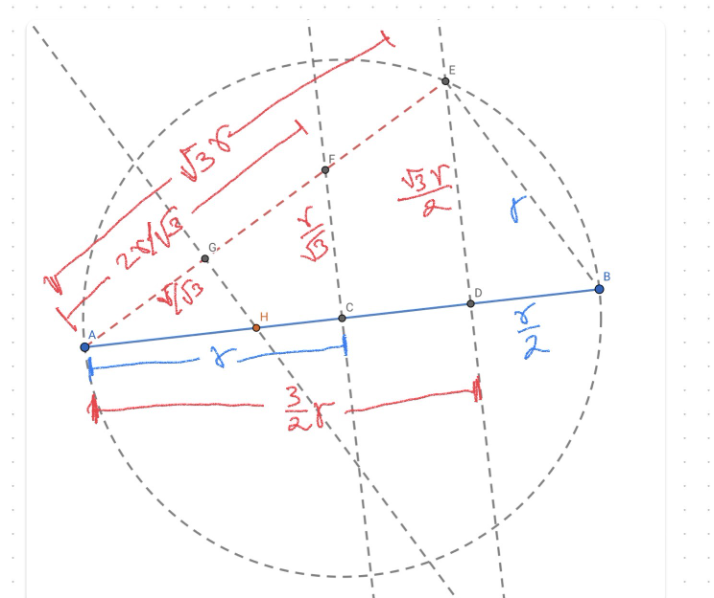
El Modelo 3 muestra los trazos que debemos hacer para dividir un segmento en razón 1:2. AH es la mitad del segmento HB, o viceversa, HB tiene el doble de longitud que el segmento AH. Los trazos que hicimos para lograr la tarea solicitada fueron mediatriz, mediatriz, circunferencia, segmento y mediatriz. Una vez que hemos logrado hacer los trazos correctos con regla y compás, la pregunta que surje es ¿cómo se argumenta o justifica que los trazos elaborados nos permiten dividir el segmento en dos partes que se encuentran a razón de 1:2?

Argumentación

Argumentar que el segmento AH es la mitad de HB es equivalente a argumentar que AH es una tercera parte de AB. Esto nos da la siguiente idea: Si se demuestra que el triángulo AGH es semejante al triángulo AEB, entonces solo tendremos que verificar que la proporción que hay entre el primero respecto al segundo es de 1:3. Lo primero es mostrar que el triángulo AGH es semejante al triángulo AEB, para ello solo basta probar que dos de sus ángulos son congruentes: 1. El ángulo HAG es congruente al ángulo BAE porque lo comparten. 2. El ángulo AGH es recto porque la recta GH es perpendicular al segmento AE. 3. El ángulo AEB es recto porque el triángulo AEB tiene un de sus lados sobre el diametro de una circunferencia y un vértice sobre la misma (ver demostración: https://youtu.be/LP5qnXKZk58). 4. El ángulo AGH es congruente con el ángulo AEB porque ambos son de 90 grados. 5. Por lo tanto, el triángulo AGH es semejante al triángulo AEB. Lo segundo es mostrar que

, que es equivalente a mostrar que

Imagen

Operaciones

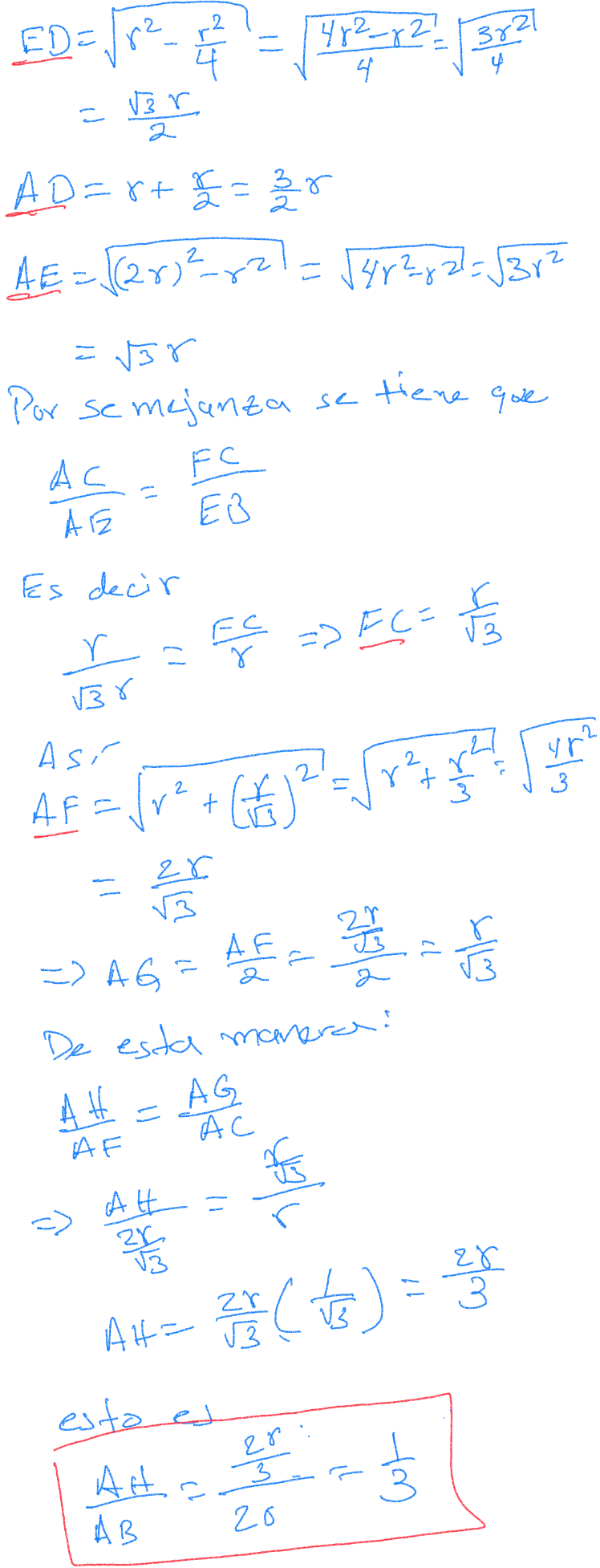
Reflexiones finales

En este apartado se espera que hablen un poco más sobre otras relaciones o patrones que identificaron en su modelo, por ejemplo: 1. ¿Qué ángulo se forma entre el segmento AB y la recta AF (o segmento AE)? Para responder esta pregunta pueden utilizar la herramienta de medir ángulo, y una vez que se determine la medida, buscar una justificación matemática de por qué mide eso el ángulo. 2. ¿Cómo se puede dividir el segmento en 5 partes iguales?¿En 6 partes iguales? ¿En 7? La idea aquí es que intenten ver si el procedimiento encontrado en este problema puede generalizarse. Si no es posible, ¿qué otro procedimiento existe que permita dividir un segmento en tantas partes iguales se desee?. En resumen, este apartado es para hablar de otras cosas que encuentran en su modelo y en el problema; es decir, es intentar de no limitarse de llegar a la respuesta y ya.